Regressão linear no aprendizado de máquina Python
Nosso objetivo educacional hoje é expandir nosso conhecimento sobre a regressão linear Python Ml com exemplos.
O que é regressão?
Quando você procura uma relação entre variáveis, usa o termo regressão.
Essa relação é usada em Machine Learning e em modelagem estatística para prever acontecimentos futuros.
Regressão linear em Python
Um algoritmo de regressão linear é um algoritmo de aprendizado de máquina baseado em aprendizado supervisionado – o programa realiza uma análise de regressão.
Um modelo de regressão prevê um valor alvo com base em variáveis independentes . A previsão é determinada principalmente por como as variáveis se relacionam umas com as outras.
As variáveis dependentes e independentes são consideradas de forma diferente em diferentes modelos de regressão, assim como o número de variáveis independentes.
Muitos nomes podem se referir à variável dependente de uma regressão.
As variáveis podem ser chamadas de variáveis de resultado, variáveis de critério, variáveis endógenas ou regressões.
As variáveis exógenas podem ser regressoras, variáveis preditoras ou variáveis preditoras.
O processo de regressão linear desenha uma linha reta através de todos os pontos de dados com base em sua relação.
Os valores futuros podem ser previstos usando esta linha.
Um aspecto muito importante do Machine Learning é a capacidade de prever o futuro.
Como funciona a regressão linear?
A linguagem Python permite que os usuários encontrem relacionamentos entre pontos de dados e desenhem linhas de regressão linear . Deixe-nos mostrar como
É mais fácil usar esses métodos do que trabalhar com fórmulas matemáticas.
As empresas são representadas pelo eixo x e o desempenho é representado pelo eixo y no exemplo abaixo.
18 empresas foram cadastradas e tiveram seu desempenho avaliado ao passar por uma cabine de pedágio. Aqui está um teste de regressão linear que podemos fazer com os dados que coletamos:
Exemplo de imagem de regressão linear:
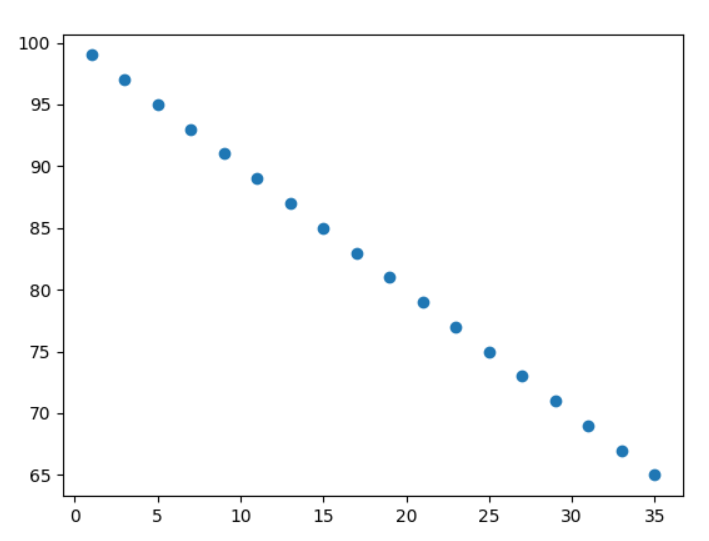
Desenhar um gráfico de dispersão é o primeiro passo:
Example
Você pode importar o Scipy e desenhar uma linha de regressão linear da seguinte maneira:
Example
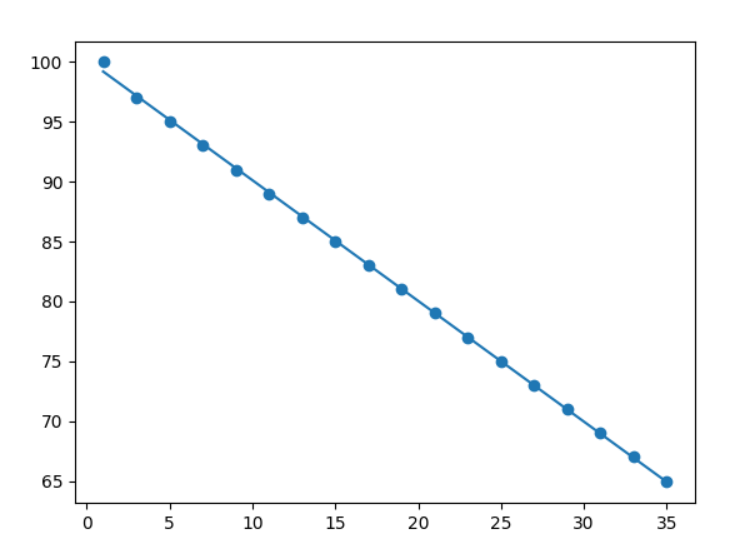
Resultado:
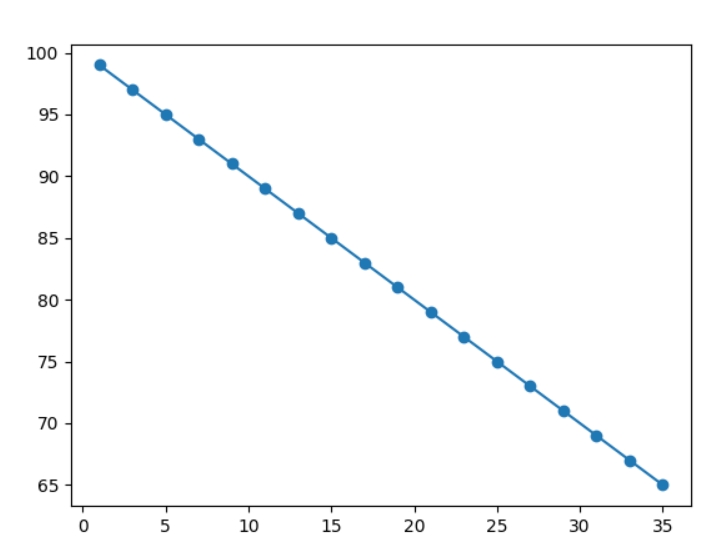
Explicação do exemplo
Você será solicitado a importar os módulos necessários.
Os módulos Matplotlib e SciPy são abordados em nossas postagens Matplotlib e SciPy .
import matplotlib.pyplot as plt
from scipy
import stats
Os valores dos eixos x e y devem ser representados por matrizes – usamos mrx como x e amplo para o eixo y da seguinte forma:
mrx = [1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35]
ample = [99,97,95,93,91,89,87,85,83,81,79,77,75,73,71,69,67,65]
Execute um método de regressão linear que retorne alguns valores-chave significativos:
slope, intercept, r,
p, std_err = stats.linregress(mrx, ample)
Faça uma função que retorne um novo valor baseado em inclinação e interceptação .
Um novo valor representa a localização do valor x correspondente no eixo y :
def pymlfunc(mrx):
return slope * mrx + intercept
A função deve ser executada para cada valor na matriz mrx. Como resultado, uma nova matriz será criada com novos valores para o eixo y:
firms = list(map(pymlfunc, mrx))
Crie o gráfico de dispersão original desenhando o seguinte:
plt.scatter(mrx, ample)
Usando a equação de regressão linear, desenhe uma linha:
plt.plot(mrx, firms)
Por fim, exiba o diagrama da seguinte maneira:
plt.show()
R – Relacionamento
A regressão linear não pode ser usada para prever nada se não houver relação entre os valores do eixo x e os valores do eixo y .
Coeficientes de correlação, como r , são usados para medir essa relação.
Um valor r de -1 a 1 indica que não há relação, enquanto 1 (ou -1) indica 100% de relação.
Você só precisa fornecer ao Python e ao módulo Scipy o mrx e amplos valores de variáveis para calcular esse valor.
Meu modelo de regressão linear se ajusta bem aos meus dados?
Example
O resultado -1,0 indica que existe uma relação de 100% e indica que a regressão linear pode ser usada no futuro para fazer previsões.
prever o futuro
Nossos dados coletados agora podem ser examinados para prever valores futuros.
Considere uma empresa de 20 anos e tente prever seu desempenho.
Usando a função pymlfunc() do exemplo anterior, podemos conseguir isso:
def pymlfunc(mrx):
return slope * mrx + intercept
Uma empresa com 20 anos terá o seguinte desempenho:
Example
Como podemos ver no diagrama, o exemplo previu um desempenho de 80:
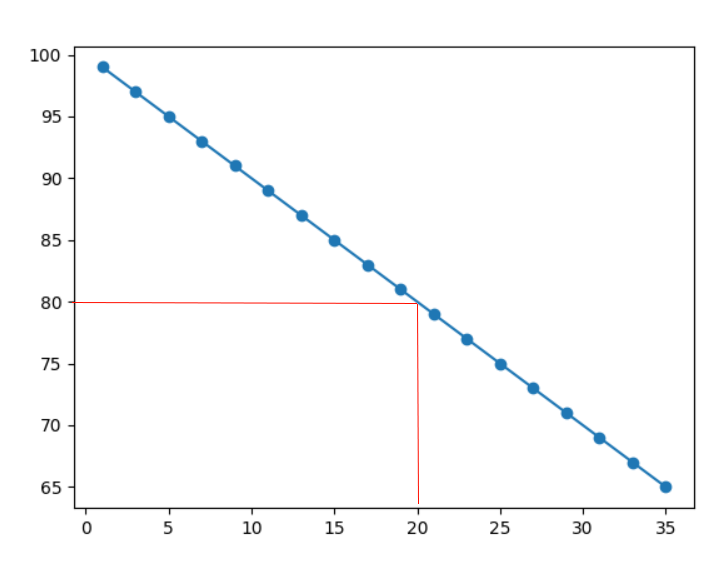
O desempenho de uma empresa com cinco anos é agora previsto:
Uma empresa com apenas 5 anos terá o seguinte desempenho:
Example
Este exemplo previu um desempenho de 95%, como pode ser visto no diagrama abaixo:
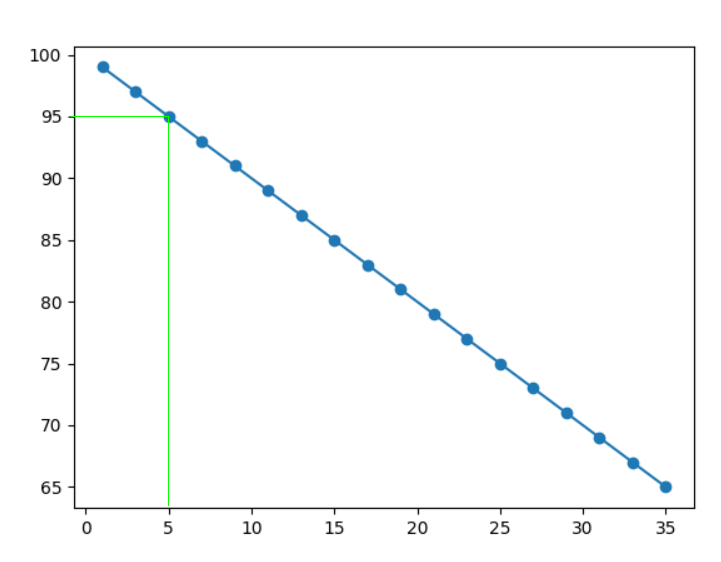
Com base em nossa previsão , descobrimos que as novas empresas cresceram muito mais rápido do que as antigas.
Ajuste ruim?
Aqui está um exemplo em que a regressão linear pode não ser a melhor forma de previsão quando se trata de prever valores futuros.
A regressão linear deve ser muito mal ajustada com esses valores para os eixos x e y:
Example
Resultado:

Que tal o r para relacionamento?
Um valor de r extremamente baixo deve ser obtido.
Example
De acordo com os resultados, 0,0364 representa uma relação muito ruim entre as duas variáveis e nos mostra que o conjunto de dados pode não ser adequado para a regressão linear usando este método.
