Distribuição Aleatória de Poisson Numpy
A função NumPy random Poisson gera números aleatórios seguindo uma distribuição de Poisson. Neste artigo, examinaremos o que é a distribuição de Poisson e como usar a função de Poisson aleatória do NumPy.
O que é uma distribuição de Poisson?
A distribuição de Poisson é uma distribuição de probabilidade discreta que expressa a probabilidade de um determinado número de eventos ocorrer em um intervalo fixo de tempo ou espaço, assumindo que os eventos são independentes e que a taxa média de ocorrência é constante.
A distribuição de Poisson é frequentemente usada para modelar ocorrências aleatórias, como:
- Número de clientes que chegam a uma loja.
- Número de carros que passam por uma cabine de pedágio.
- Número de chamadas telefônicas recebidas por um call center.
A distribuição de Poisson é caracterizada por um único parâmetro, que representa a taxa média de ocorrência dos eventos.
Este parâmetro é denotado por λ ( lambda ) e também é igual à variância da distribuição.
A função massa de probabilidade ( PMF ) da distribuição de Poisson é dada por:
P(mrX = k) = (e^(-λ) * λ^k) / k!
onde mrX é a variável aleatória que representa o número de eventos, k é um inteiro não negativo, e é a base do logaritmo natural ek! é o fatorial de k.
Função aleatória de Poisson NumPy
Uma função Poisson aleatória Numpy é uma distribuição discreta e faz parte do módulo NumPy.random e é usada para gerar números aleatórios seguindo uma distribuição Poisson.
Ele estima quantas vezes um evento pode ocorrer em um determinado período de tempo.
Por exemplo, qual é a chance de uma pessoa comer quatro refeições por dia se ela comer três refeições diariamente?
Um parâmetro desta função é o seguinte:
| Parâmetros | Visão geral |
| eu sou | O número de instâncias ou a taxa de eventos, por exemplo. Três na situação acima. |
| tamanho | É assim que a matriz será organizada quando for recuperada. |
Sintaxe
numpy.random.poisson(lam=1.0, size=None)
onde lam é o valor esperado da distribuição de Poisson e size é a forma da matriz de saída.
A função retorna uma matriz de números inteiros aleatórios representando o número de eventos que ocorrem em um intervalo fixo de tempo ou espaço.
Os valores na matriz são gerados independentemente uns dos outros e seguem uma distribuição de Poisson com parâmetro λ .
Vejamos os exemplos abaixo:
Crie uma distribuição aleatória 1 × 30 para a instância 3:
Example:
Distribua aleatoriamente os resultados de 5 da seguinte forma:
Example:
Visualização da Distribuição de Poisson
Para visualizar a distribuição NumPy Random Poisson, podemos usar a biblioteca matplotlib do Python .
Vamos gerar um intervalo de valores para o número de ocorrências e, em seguida, calcular a função de massa de probabilidade para cada valor usando a fórmula de distribuição de Poisson.
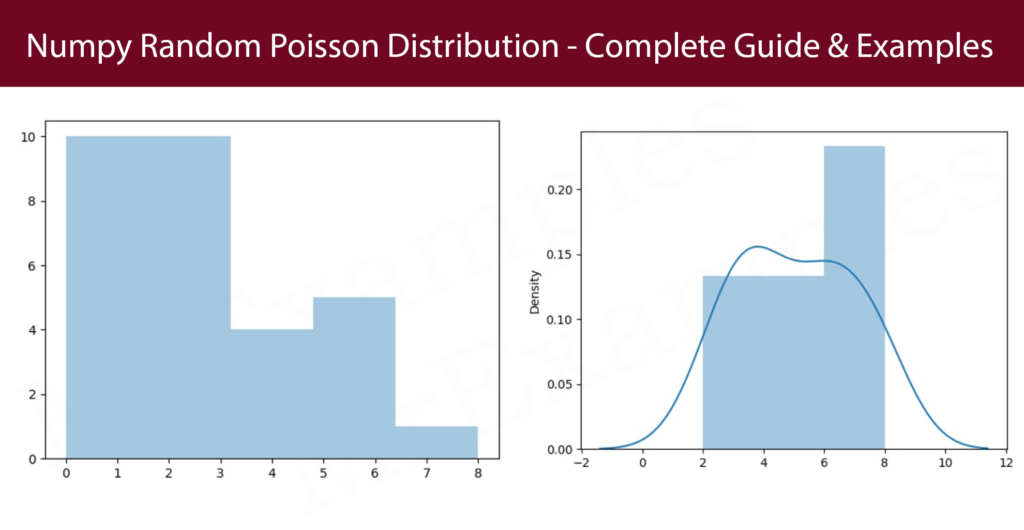
Por fim, traçaremos os resultados como um histograma.
Implementação de representação visual:
Example:
Aplique o código abaixo com kde = True :
Example:
Diferença entre distribuição normal e de Poisson
No Numpy random poisson, a distribuição normal é contínua , enquanto a distribuição de poisson é discreta .
Quando a distribuição de Poisson crescer suficientemente larga e longa, ela se tornará quase idêntica à distribuição normal com apenas alguns desvios padrão e médias.
As diferenças entre as distribuições normal e de Poisson podem ser resumidas da seguinte forma:
- A distribuição normal é usada para dados contínuos, enquanto a distribuição de Poisson é usada para dados de contagem.
- A distribuição normal possui dois parâmetros (média e desvio padrão), enquanto a distribuição de Poisson possui um parâmetro (taxa média de ocorrência).
- A distribuição normal é simétrica em torno da média, enquanto a distribuição de Poisson é assimétrica para a direita se a taxa média de ocorrência for pequena.
- A distribuição normal tem uma função de densidade de probabilidade contínua, enquanto a distribuição de Poisson tem uma função de massa de probabilidade discreta.
- A distribuição normal mede a dispersão dos dados usando o desvio padrão, enquanto a distribuição de Poisson tem uma variância fixa igual à taxa média de ocorrência.
Os dois exemplos abaixo garantirão que você entenda a diferença entre distribuição Normal e Poisson:
Example:
Example:
Diferença entre distribuição de Poisson e distribuição binomial
Uma diferença muito pequena é encontrada entre as distribuições binomial e de poisson, e é que a distribuição binomial é aplicada para testes discretos , enquanto a distribuição de poisson é utilizada para testes contínuos .
No entanto, quando n é muito alto e p está próximo de 0 , a distribuição binomial é quase igual à distribuição de poisson, de modo que n + p é aproximadamente idêntico a lam .
As diferenças entre as distribuições de Poisson e binomial podem ser resumidas da seguinte forma:
- A distribuição de Poisson é usada para dados de contagem, enquanto a distribuição binomial é usada para o número de sucessos em um número fixo de tentativas .
- A distribuição de Poisson tem um parâmetro (taxa média de ocorrência), enquanto a distribuição binomial tem dois parâmetros (probabilidade de sucesso e número de tentativas).
- A distribuição de Poisson é assimétrica à direita se a taxa média de ocorrência for pequena, enquanto a distribuição binomial é simétrica se p=0,5.
- A distribuição de Poisson tem um PMF que depende apenas do parâmetro de taxa, enquanto a distribuição binomial tem um PMF que depende tanto da probabilidade de sucesso quanto do número de tentativas.
- A distribuição de Poisson é usada para aproximar a distribuição binomial quando o número de tentativas é grande e a probabilidade de sucesso é pequena.
Aqui estão dois exemplos que demonstram a distinção entre as distribuições Poisson e Binomial:
Example:
Example:
Conclusão
A função NumPy random Poisson é útil para gerar números aleatórios seguindo uma distribuição de Poisson.
Ele pode ser usado em uma variedade de aplicações, como simular chegadas de clientes, chamadas telefônicas ou acidentes de carro.
Compreendendo a distribuição de Poisson e como usar a função NumPy random Poisson, podemos analisar e modelar melhor as ocorrências aleatórias em nossos dados.
